First-Order Low-Pass Filter Discretization

#1 : Interactive Low-Pass Filter Studio #2 : Article - The Basics #3 : Article - Design & Discretization #4 : Article - MatLab Script

Interactive Low-Pass Filter Studio

The scope is clickable & draggable - interactive demo is here.

Bode plot of the discrete low-pass filter (interactive).

Low-Pass Filter Design

The Basics

It has occurred to me that most engineers and scientists are quite familiar with the basic formula of an infinite-impulse response (IIR) low-pass filter (LPF):

$$y[k] = a \times y[k-1] + (1-a)\times x[k],$$

(1)

This low-pass filter variation is easy to implement on processors or FPGAs.

Also, such filter should in some way correspond to the following first-order continuous-time transfer function:

$$H(s) = \frac{\omega_c}{s+\omega_c},$$

(2)

In this short tutorial, we will derive the relationship between the corner frequency "omega" in the continuous time domain and the "a" coefficient in the sampled time domain.

First-order IIR Low-pass Filter Design & Discretization

Determine the corner frequency of your low-pass filter. The corner frequency should be at most 10% of the system sample rate.
Discretize- use the "zero-order hold" approach. The reason to use this approach is to emulate the sample & hold behavior:

A continuous-time domain filter with input and output signals is shown below:
pcc2

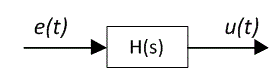
Continuous-time domain signals and a digital filter are represented as:
pcc2

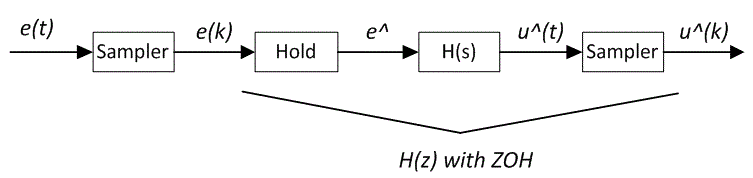
The formula to discretize a transfer function preceded by a zero-order hold follows:

$$H(z) = \frac{z-1}{z}Z\Big(L^{-1}\big(\frac{H(s)}{s}\big)\Big),$$

(3)

From Laplace to Z-domain lookup table:

$$Z\Big(L^{-1}\big(\frac{H(s)}{s}\big)\Big) = Z\Big(L^{-1}\big(\frac{\omega_c}{s(\omega_c+s)}\big)\Big) = \frac{z(1-e^{-\omega_cT})}{(z-1)\times(z-e^{-\omega_cT})},$$

(4)

Therefore:

$$H(z)=\frac{Y(z)}{X(z)}=\frac{1-e^{-\omega_cT}}{z-e^{-\omega_cT}},$$

(5)

A bit more rearranging leads to:

$$Y(z)(z-e^{-\omega_cT})=X(z)(1-e^{-\omega_cT}),$$

(6)

The next step is to take an inverse Z-transform:

$$y[k+1]-y[k]e^{-\omega_cT}=x[k](1-e^{-\omega_cT}),$$

(7)

And shift by one sample:

$$y[k] = y[k-1]e^{-\omega_cT} + x[k-1](1-e^{-\omega_cT}),$$

(8)

Hence:

$$a = e^{-\omega_cT}$$

(9)

MatLab script

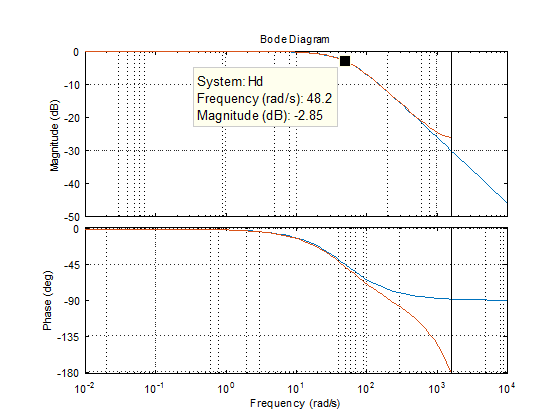
A basic MatLab script (below) verifies the equivalency between the continuous transfer function and its discrete time-domain counterpart.

Note that the sampling rate was chosen as 500 Hz and the break frequency as 50 rad/s or ~8 Hz.

MatLab(©) Code

% First-order Low-Pass Filter Discretization
%
% Control Systems Academy team
%
% 6/25/2017

clc; format compact

% Continuous time filter
s = tf('s');
w = 50; % rad/s

H = w/(s+w)

T = 1/500;
Hd = c2d(H,T,'zoh')

opts = bodeoptions;
opts.FreqUnits = 'rad/s';
opts.XLim = [0.01, 10000];
opts.Grid = 'on';

bode(H,Hd, opts)

% no more

Magnitude and Phase Bode plots of a continuous low-pass filter with corner frequency 50 rad/s. The discrete counterpart has 200 Hz sampling frequency.
pcc2

Thought Nuggets

Q: Can IIR (infinite-impulse response) filters become unstable?

A: Yes. These filters have a negative-feedback path and a single incorrect parameter computation can result in oscillations or output out-of-bound instability.

The benefit of IIR filters is their ease of use with constant coefficients and a simple transfer function representation.
FIR filters are generally used in more advanced digital signal processing (DSP), such as in transceivers.

Change log

6/25/2017

Initial article release.

4/30/2019

Clarified the relationship between the parameter "a" and the corner frequency "omega"