Bode Plot Engine Documentation
Table of Contents
Introduction
The aim of the Bode Plot Engine is to emulate MatLab's(r) by MathWorks(c) ability to parse and plot the magnitude and phase of continuous transfer functions. The Bode Plot Engine is a computing and plotting environment with combined symbolic and numerical inputs. The purpose behind providing the engine is simple: not everyone has access to MatLab. Alternatively, there might not a free license at the time or simply one would like to explore the design of control systems online on a machine without installed MatLab.
Bode Plot Engine structure
The Bode Plot Engine consists of these self-explanatory blocks:
- Editor
- Console
- Console Log
- Magnitude & Angle Plot
- Variable log
Syntax
The syntax is mostly cross-compatible with MatLab.
Engine Control
- clf; Clears the figure
- clc; Clears the console
- clear; Clears the variable repository
- Also accessible as buttons:
Help
- Just type "help" either in the console in the editor window (and then execute)
Numerical input
- e.g., H1 = 0.0022;
- e.g., H2 = 22e-4; scientific notation is now supported! (1/29/2018)
Variable assignment
- E.g., H = 1/s^3; Max Laplace operator "s" power: 9
- Laplace operator "s" power cannot be negative!
- E.g., H2 = H+s;
Plotting
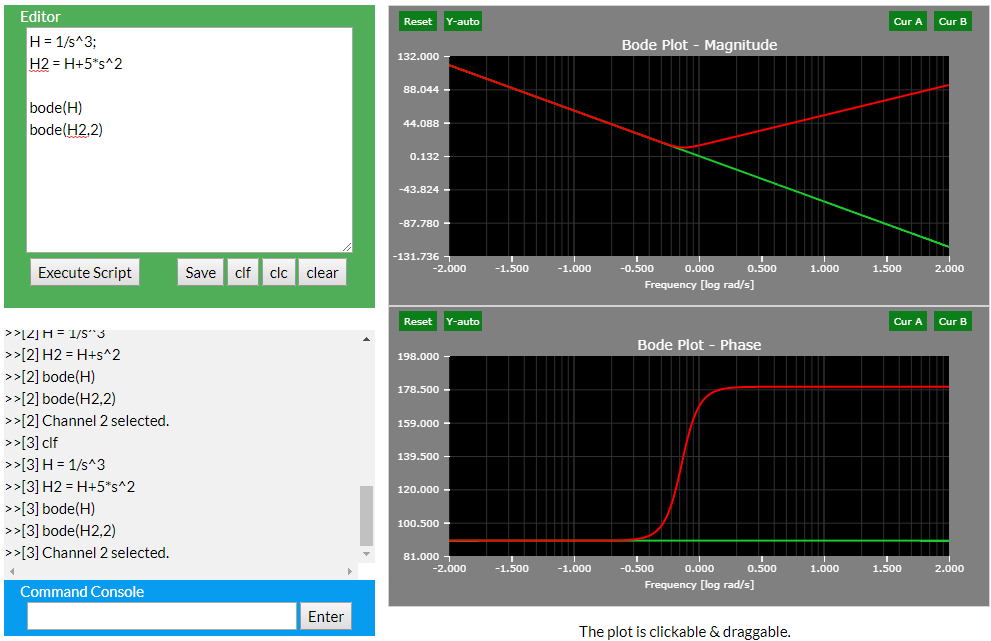
- bode(H) - plots function H in green.
- bode(H2,2) - plots function H2 in red. The color sequence is:
1st plot
2nd plot
3rd plot
4th plot
5th plot
6th plot
- bode(H2,4) - plots function H2 in yellow. Up to 6 waveforms can be displayed at a moment.
H = 1/s^3;
H2 = H+5*s^2
bode(H)
bode(H2,2)
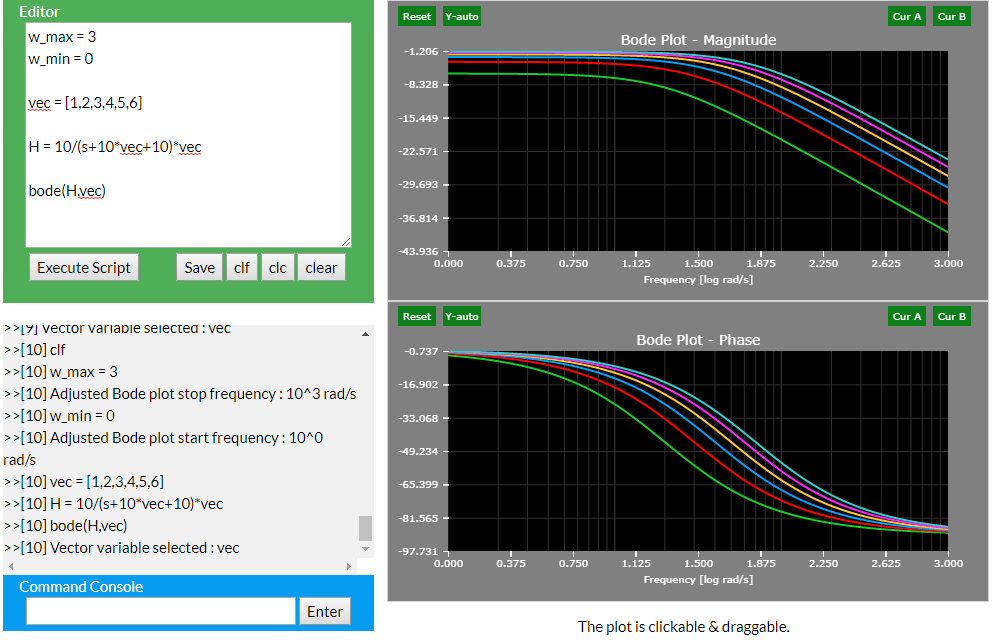
Vectorization
- Multiply an expression by a vector: vec = [1,2,3]
- Up to 6 waveforms can be displayed at once.
- E.g., H2 = H+5*s^2;
w_max = 3
w_min = 0
vec = [1,2,3,4,5,6]
H = 10/(s+10*vec+10)*vec
bode(H,vec)
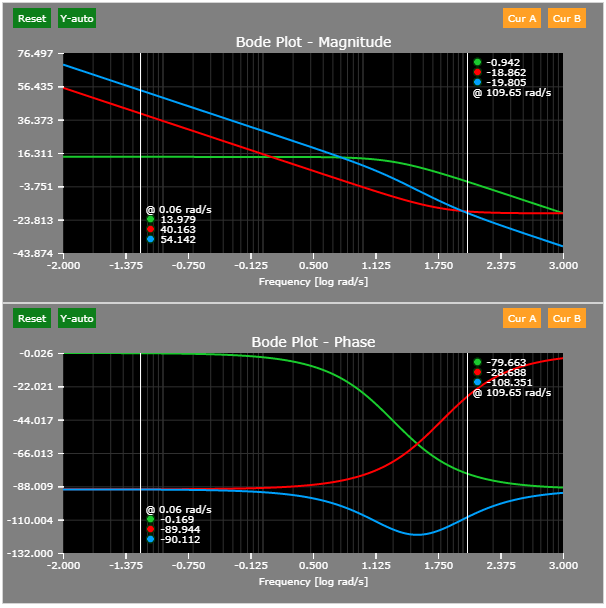
Cursors
- Up to two cursors can be activated at a time. The same cursor is displayed in both the magnitude and angle plots.
Variables
- All stored variables are shown in the Variable Repository.
- Each variable has four values: ID, Name, Input, and Parsed Value

Supported / Not Supported Syntax
| Syntax | Remark |
|---|---|
| s^-1 | Not supported. Please use 1/s instead. |
| 6^3 | Not supported. Please use 6*6*6 instead. |
| s^x, x>9 | Not supported. Please use MatLab for extreme case transfer functions. JavaScript does not have the required numerical precision. |
| % this is a comment | Such line is not parsed. |
Examples
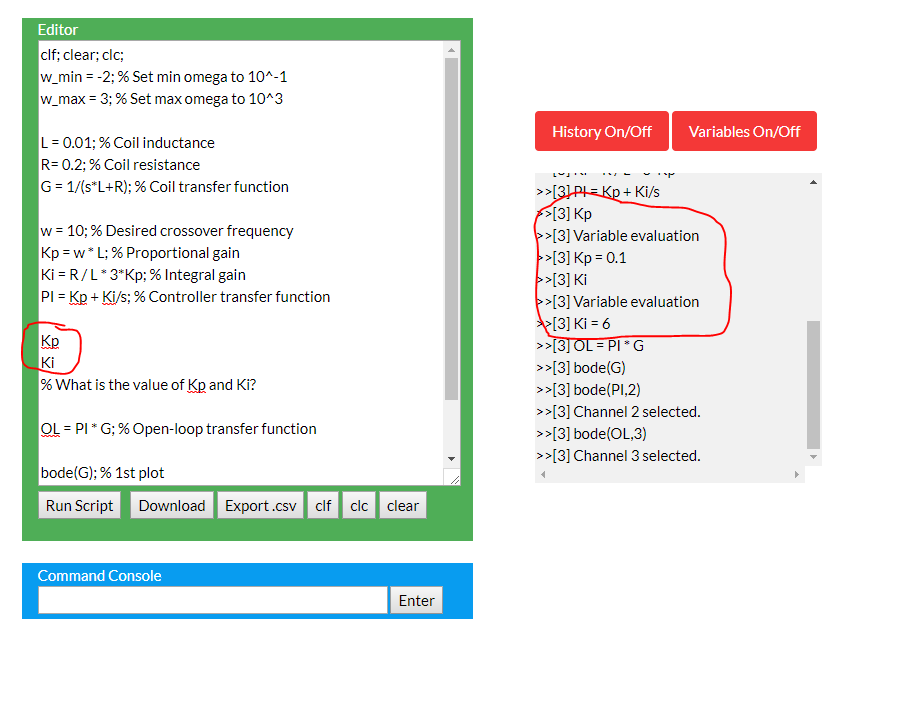
The following example shows the design of a simple closed-loop coil current controller:
clf; clear; clc;
w_min = -2; % Set min omega to 10^-1
w_max = 3; % Set max omega to 10^3
L = 0.01; % Coil inductance
R= 0.2; % Coil resistance
G = 1/(s*L+R); % Coil transfer function
w = 10; % Desired crossover frequency
Kp = w * L; % Proportional gain
Ki = R / L * 3*Kp; % Integral gain
PI = Kp + Ki/s; % Controller transfer function
OL = PI * G; % Open-loop transfer function
bode(G); % 1st plot
bode(PI,2); % 2nd plot
bode(OL,3); % 3rd plot
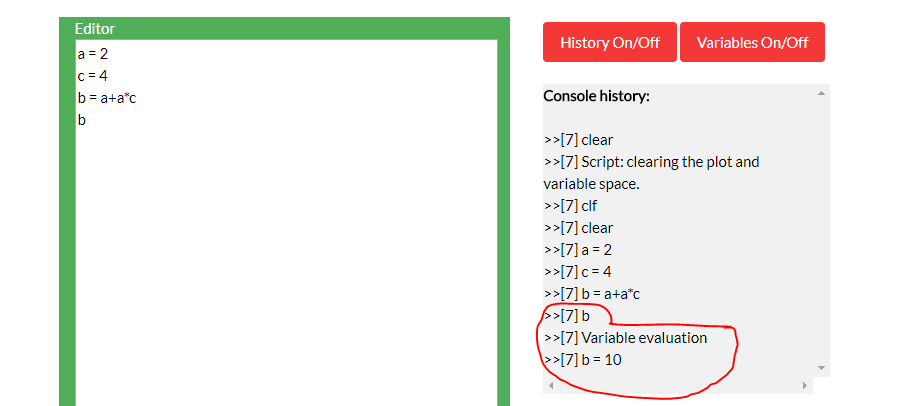
Variable Evaluation
It is possible to use the Bode Plot Engine as a calculator - that is, all symbolic variables can be evaluated and displayed.
Two examples are shown below:
Behind the Scene
Variable Repository
Each variable is stored as an array with four variables: ID, Name, Input, and Parsed Value
- ID
- Each variable has a unique ID starting with 000 (max number of IDs is 1,000)
- When parsed, the variable name is replaced with #ID, e.g., #004
- Name
- Name as set by the user
- Input
- Variable expression as set by the user
- Parsed Value
- All variables are replaced by their unique variable IDs
- All Laplace operators are replaced by $X operators, where "X" is the operator power. E.g., s^2 is $2
- Expressions are wrapped in parentheses to enable parsing with correct operator precedence (FORTRAN I algorithm used - see this Article on WiKi)

Change log
12/1/2017
- Started work on the Bode Plot Engine.
1/29/2018
- Scientific input notation verified.
4/15/2018
- Script is now part of the URL for easy sharing.
4/22/2018
- Each script call now automatically clears both the variable space and figures. This prevents issues with wrong variable declaration order.
7/15/2018
- Symbolic variables can now be evaluated.