Introduction

Transfer function stability is solely determined by its denominator. The roots of a denominator are called poles.

Poles located in the left half-plane are stable while poles located in the right half-plane are not stable.

The reasoning is very simple: the Laplace operator "s", which is location in the Laplace domain, can be also written as:

Left half-plane has negative sigma.

For a first-order system, the following transfer function corresponds to this time domain differential equation:

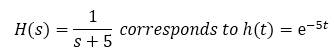
Consider a step change as the input:

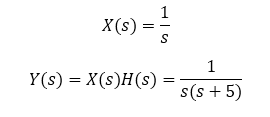
Hence:

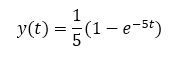
The output converges to 0.2, a steady-state and stable value.

Stability of a Generic Polynomial

Generally, consider the following generic denominator:

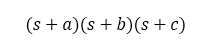
If such a polynomial is expanded and terms are collected, we obtain:

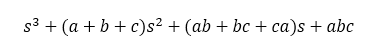
Claim: If all polynomial coefficients are positive, all roots are negative and the system is stable

In short:

• If all polynomial coefficients are positive, then all poles are negative.
• If all roots are negative, then all polynomial coefficients are positive.

If all three terms a, b, and c are positive, then all three poles are located in the left-half plane and the system is stable. Also, notice that all coefficient of the expanded polynomial are positive.

E.g., a = 7, b = 2, c = 4, (poles are located at -7, -2, and -4).

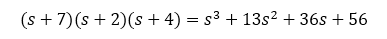
For a polynomial containing complex poles as shown below, the imaginary part sign does not matter since there needs to be the complex pole counterpart.

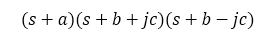
Thus, it suffices that a and b are positive:

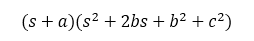
How do we know that the second polynomial (s²+2bs+b²+c²) has negative roots?

The b² and c² terms are always positive and the b term is positive as indicated above.

Therefore, if all coefficients are positive, all roots are negative and the system is stable.

Claim: If any polynomial coefficient is negative, at least one root is positive and the system is unstable

Without a proof here.

Claim: If a polynomial coefficient is zero, at least one root is positive and the system is unstable

See the following polynomial:

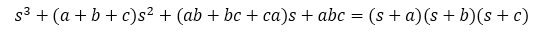
Case 1: s²(a+b+c) = 0

This means that at least one term (from a, b, c) is negative, otherwise the sum would be positive.

Case 2: s(ab+bc+ca) = 0

From the way the coefficient is structured, at least one term has to be negative or all three terms need to be zero otherwise the coefficient would be positive.

Case 3: abc = 0

This term can be zero. This also means that at least one root is zero as well.

e.g. a = 0

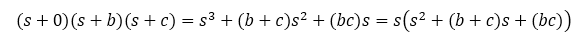
Major takeaway: based on this analysis (by no means a complete proof) when a coefficient of a power of s is zero, then the system is unstable.

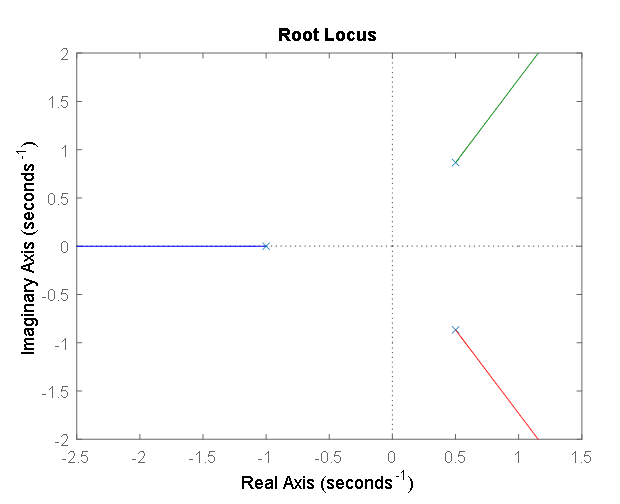
Consider the following system. For which gain Kp does the closed-loop system becomes stable?

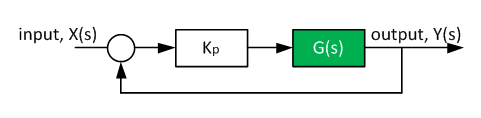
The plant transfer function G(s) is shown below:

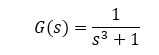
The complete closed-loop transfer function, including the proportional controller Kp, is:

Answer: No proportional controller gain can make the system stable since the closed-loop transfer function has zero "s" and "s²" term coefficients. All coefficients of "sⁿ" must be positive.

Root locus follows (notice the two right half-plane poles).

Further Reading

Proportional Controller Implementation

In MatLab, DSPs, and FPGAs.

Control System Block Diagram

The fundamentals of signal flow.

System Modeling With Transfer Functions

Introduction to dynamic systems.

Fourier Series Demo

It is all sine waves.