How to run the simulation - 3 steps

1. There are two individual systems with different preloaded loads - a) with no damping and b) with damping
2. Hit the "Run" button and observe the system response for both systems
3. Modify the proportional gain to observe the effect on steady-state error and dynamic response

Theory

One step beyond On-Off systems

• The proportional controller is the simplest linear controller - linear since the output is linearly proportional to the input of the controller.
• Look at the block below - the input to the proportional controller is the difference between the desired output and the actual output.
• The larger the difference, the larger the force the controller commands as it tries to correct for the error.
• If there is no error, the output of the controller is zero.

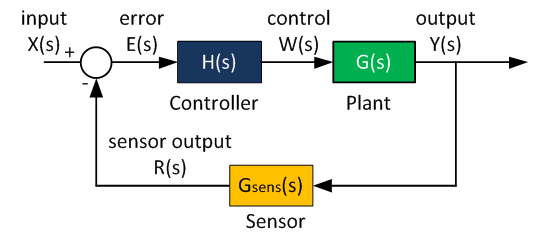
On the dynamics of Proportional Controllers

• The plant in the simulation is of first order. Since the controller is not dynamic (it does not integrate or differentiate), the overall system order is 1 as well.
• First-order system do not oscillate or experience overshoot.
• Increasing the controller gain makes the system more aggressive:
  • It will track much better than systems with low gains.
  • Also, it will track the reference much faster.
  • If there is damping in the system (second example), a gain increase will reduce the steady-state error. However, the error will never come down to zero without an integrator in the controller or another compensation technique, such as virtual reference decoupling.
  • This is typically not a problem for first order systems; however, an increase of gain can quickly destabilize higher order systems.

Driving Current Through an Inductive Load

• E.g., through motor windings, an inductive heating element, or an MRI coil

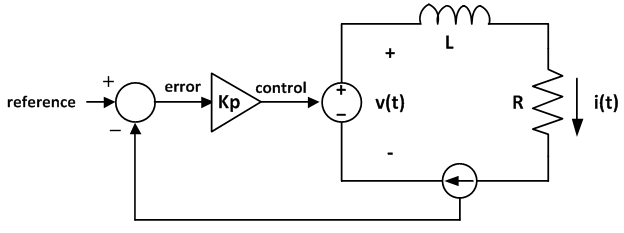
• The proportional controller sets the output voltage of an amplifier.
• The amplifier applies voltage across a coil L with parasitic resistance R
• In steady-state, the coil voltage is:

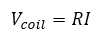
• Coil voltage is equal to the amplifier voltage:

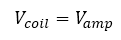
• And the output of the controller is:

• Rearranging terms to obtain the ratio of coil current to the reference current:

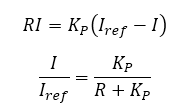
• Hence, with no parasitic resistance (R = 0 Ohm), the coil current always perfectly follows the reference current! Note that is only happens in steady-state. See the SYSTEM MODELING WITH TRANSFER FUNCTIONS article to learn more about system dynamics.
• Alas, the parasitic resistance is virtually never zero. Hence, the proportional controller cannot achieve zero steady-state error.
• However, if the ratio of Kp to R is reasonably high (say 10:1), the steady-state error is small (below 10%).
• In other words, small gains produce inaccurate systems.

References

This page is a modification of a now non-existent page located at:
http://www.facstaff.bucknell.edu/mastascu/eControlHTML/Intro/IntroNotes/IntroNote_VeryBasic_PropCont.htm

Version

Version of this article is 10/02/2017.

Further Reading

Proportional Controller Implementation

In MatLab, DSPs, and FPGAs.

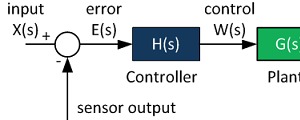
Control System Block Diagram

The fundamentals of signal flow.

System Modeling With Transfer Functions

Introduction to dynamic systems.

Fourier Series Demo

It is all sine waves.